MATEMÁTICA SUPERIOR

Cálculo de límites, con y sin indeterminaciones

El límite de una función nos proporciona información sobre su comportamiento. Por ejemplo, sobre su continuidad y las posibles asíntotas.

En esta página vamos a ver las reglas básicas para operar con infinitos, las indeterminaciones y algunos procedimientos para evitar las indeterminaciones. Finalmente, resolvemos 50 límites de forma detallada.

Es importante destacar el concepto de indeterminación o forma indeterminada:

Una indeterminación o forma indeterminada es una expresión algebraica que a veces aparece en el cálculo de límites y cuyo valor no se puede predecir, depende de la función del límite a calcular.

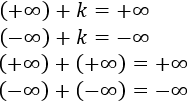
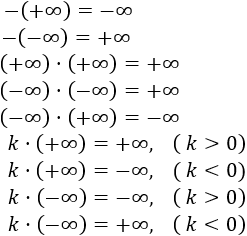
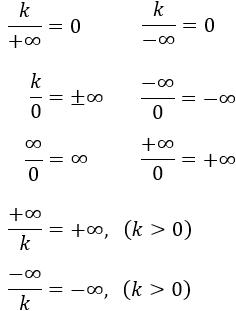
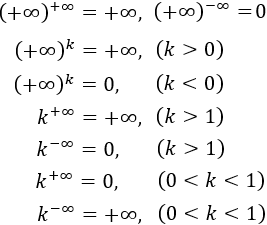
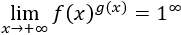
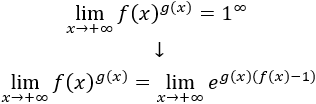
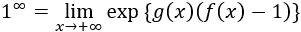
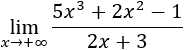
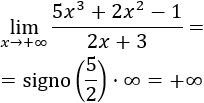
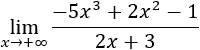
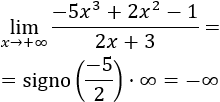
Por ejemplo, si una función tiende a $5/\infty$, entonces su límite es $0$. Sin embargo, no sabemos de antemano el límite de una función que tiende a $\infty /\infty$ (podría ser infinito o un valor finito). Por esta razón, decimos que $\infty /\infty$ es una indeterminación.

Recordad que

• el límite de $f\left(x\right)$ cuando $x$ tiende a $a$ es $f\left(a\right)$ si existe $f\left(a\right)$,
• el límite cuando $x$ tiende a $a$ existe si y sólo si existen los límites laterales por la izquierda y la derecha de $a$ y coinciden.

Finalmente, comentamos que existen métodos más sencillos y rápidos de calcular límites y evitar las indeterminaciones, como son la regla de L'Hôpital (cálculo diferencial) y los infinitésimos equivalentes.

Operaciones con infinitos

Reglas para sumar, restar, multiplicar, dividir o elevar con infinitos. Estas son las operaciones cuyo resultado se puede predecir (al contrario que las indeterminaciones).

Sea $k$ un número real distinto de $0$.

Sumas:

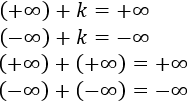
La resta es análoga. Por ejemplo,

$$k-\infty =-\infty$$

$$k-(-\infty )=+\infty$$

Productos:

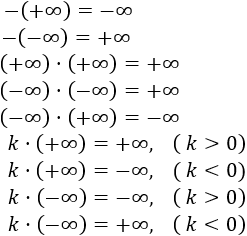
Observad que el producto de infinitos o el producto de infinito por una constante ($k\ne 0$) es infinito. El signo del resultado depende de la regla de los signos. Sin embargo, infinto por cero ($\infty \cdot 0$) es una indeterminación.

Cocientes:

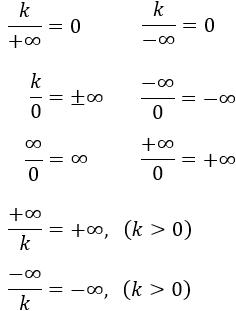
El cociente de ceros y el de infinitos es indeterminado.

Potencias:

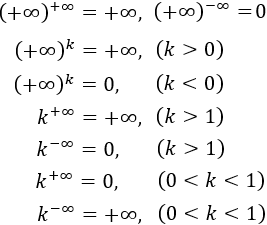
Las potencias ${\infty }^0$, $0^0$ y $1^{\infty }$ son indeterminaciones.

Indeterminaciones y procedimientos

Las siete indeterminaciones que existen son las siguientes:

Cuando aparece una indeterminación, tenemos que aplicar determinados razonamientos o procedimientos que permitan hallar el resultado del límite. A continuación, enumeramos algunos de los procedimientos:

Cero partido cero, $0/0$:

Suele aparecer en el límite de un cociente de polinomios cuando $x$ tiende a una de sus raíces comunes. En este caso, se puede simplificar el cociente y evitar así la indeterminación.

Infinito menos infinito, $\infty -\infty$:

• Si aparece en el límite de un polinomio, el resultado es infinito. Su signo depende del coeficiente del monomio con mayor grado.
• Si aparece en una resta de raíces, pueden ayudarnos las siguientes fórmulas:
  $$a-b=\frac{a^2-b^2}{a+b}$$
  $$a-b=\frac{a^3-b^3}{a^2+ab+b^2}$$
• Si aparece en una resta de funciones muy distintas (por ejemplo, un logaritmo y una exponencial o un polinomio), hay que fijarse en la función cuyo crecimiento es mayor.

1 elevado a infinito, $1^{\infty }$:

Si la función $f$ tiende a $1$ y la función $g$ tiende a infinito, entonces

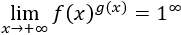
Para evitar esta indeterminación, aplicamos la siguiente fórmula:

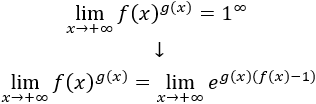
Nota 1: la fórmula funciona también con $x\to -\infty$ ó $x$ tendiendo a un número finito.

Nota 2: Es habitual escribir una exponencial $e^{h\left(x\right)}$ como $exp\left\{h\right(x\left)\right\}$ (es una cuestión de notación). Así,

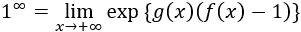
Cociente de infinitos, $\infty /\infty$:

Puede aparecer en cocientes muy variados: polinomios, raíces, exponenciales... En cada caso se procederá de forma distinta.

• Si tenemos un cociente con exponenciales, dividimos entre la exponencial cuya base sea mayor.
• Si tenemos un cociente de polinomios $P\left(x\right)/Q\left(x\right)$ siendo $p$ y $a_p$ el grado y el coeficiente principal de $P\left(x\right)$ y $q$ y $b_q$ los de $Q\left(x\right)$, entonces el límite cuando $x$ tiende a $+\infty$ es
  
  
  Observad que el resultado del primer caso es infinito, pero multiplicamos por el signo cociente de los coeficientes principales de los polinomios para saber el signo (positivo o negativo) del infinito.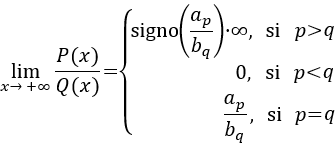
  Nota: en el caso del límite tendiendo a $-\infty$, se aplica el mismo criterio, aunque es más complicado calcular el signo en el primer caso porque depende también de si los grados de los polinomios son ambos pares (o impares) o uno es par y el otro es impar.
• Si tenemos un cociente de raíces de polinomios, aplicamos el criterio anterior, aunque el orden de las raíces divide a los grados de los polinomios.
• Si tenemos un cociente con funciones muy distintas, como puede ser un polinomio entre una exponencial o un logaritmo, es suficiente comparar el crecimiento de dichas funciones.
  Por ejemplo, como una exponencial crece más rápido que un polinomio, el límite de sus cociente es:
  
  • Infinito, si la exponencial está en el numerador.
  • Cero, si la exponencial está en el denominador.

Cero o infinito elevado a cero, $0^{\infty }$ ó ${\infty }^{\infty }$:

Normalmente, es útil aplicar logaritmos y sus propiedades:

$$limA\left(x\right)=lim{e}^{ln\left(A\right(x\left)\right)}$$

Límites resueltos

Límite 1

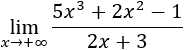
SOLUCION

Tenemos la indeterminación infinito partido infinito.

Como el grado del polinomio del numerador es mayor que el del denominador, el límite es infinito:

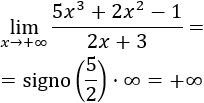
El infinito es positivo porque el cociente de los coeficientes principales de los polinomios es positivo.

Límite 2

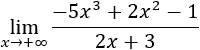
SOLUCION

Razonamos como en el límite anterior:

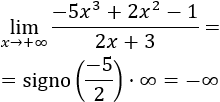
En este límite, el infinito del resultado es negativo porque el coeficiente principal del polinomio es negativo.